As we saw above, some machine learning models, often called glass box, are inherently explainable, while other black box models, like deep neural networks, require that we apply XAI techniques after they’re trained. Because the issue with black box models is complexity, we often train simpler and easier-to-understand models, called surrogate models, to explain their inner workings.
In this section, we examine two types of explainability methods: local and global. Local explainability methods can be used to explain a single instance of our model outputs – for instance, what parts of an image were most relevant to identify a picture of Garfield the cat as a cat? The local explainability methods that we examine in this chapter are LIME and counterfactual explanations and layer-wise relevant propagation (LRP).
In contrast, global explainability methods aim to explain general attributes common to all instances of model output. For example, if we use a model to predict housing prices, a global explanation could tell us how important the neighborhood is in general when the model is making predictions for the price — in other words, how much a specific feature matters to the general outcome. In this section, we take a look at sensitivity analysis (SA) and using a global surrogate model.
Both local and global explainability methods can be very useful in practice depending on the use case. If you aim to have a GDPR-compliant automated decision-making system, then every end user should be able to obtain an explanation about how a decision was made regarding their specific case, and a local explainability method l is the ideal tool for that. However, if you wish to conduct a broad-level auditing of how a model works, a global explainability method will give you a more comprehensive, birds-eye view of what features are important for producing outputs.
Model-agnostic local explainability techniques
Local explainability techniques can answer the question “Why did the model output this result, given this set of inputs?” Model-agnostic techniques, on the other hand, are techniques that can be used regardless of what type of model we're trying to explain. Let’s look at some examples.
Local interpretable model-agnostic explanations (LIME)
LIME was first proposed in a paper published in 2016 (2). The authors perturb the original data points slightly, feed them into the black box model, and then observe the corresponding changes in outputs. The perturbed input data along with the black box model outputs are then used to train a new model, called a surrogate. A surrogate model is an explainable model that’s able to mirror the behavior of the black box model and can be easily interpreted.
Generally, the steps for building the surrogate model can be summarized as follows:
Select a data instance of interest (for example an image that was classified by an image classifier) that we want to have an explanation for of the black box model’s decision (the classification made by the image classifier).
Create a new dataset for the instance of interest (for example if the instance of interest is an image, we change a few pixels in this image) and get the black box predictions for these new samples.
Weight the new samples according to their proximity to the instance of interest. The more the sample is similar to the instance of interest, the smaller the assigned weight should be. Similarity can be measured with suitable distance functions.
Train a model that’s easy to interpret (for example a linear regression model or a decision tree) on the newly created dataset.
Explain the instance of interest by interpreting this local model’s decision which is able to capture the decision-making process of the black-box model in the local region.
For more details, see the research paper here.
Model-agnostic global explainability techniques
Global surrogate models
In contrast to local surrogate models, global surrogate models aim to capture the overall behavior of a black box model. They’re model agnostic, meaning that they can be applied to explain any model. On the downside, they may be less accurate at explaining predictions of specific inputs for which local surrogate models are used.
Here we describe the steps and the theory behind global surrogate generation. First, you need a dataset that can be used for model training. This dataset can accurately train both a real black box model and a global surrogate model. You then need to retrieve the outputs predicted by the black box AI models for the selected dataset. In the next step, you need to select an inherently explainable model and train it on the dataset along with the outputs predicted by the black box model as labels. The goal is to have the surrogate model predict the outputs of the black box model – in other words, to as accurately as possible mirror the black box model’s predictions for the same data points.
Measuring surrogate model performance using R-squared error
To check how well the surrogate model approximates the black box model, one can measure how well the surrogate is able to predict the outputs of the black box model, for example by using R-squared error as described in the following.
If you recall from linear regression, we can use R-squared error in prediction against actual expected outputs as the indicator of the line for forecasting unseen data. Here we can apply the same concept to measure how the surrogate model replicates the black box model. In this context, R-squared (R²) can be calculated as follows:


The R-squared measure can be understood as the proportion of variance that the surrogate model captures. When R-squared is close to 1 (indicating low SSE), it means that the interpretable model closely predicts the behavior of the black box model. In such cases, the interpretable model may be a good interpretable surrogate for the complex model. On the other hand, if R-squared is close to 0 (indicating high SSE), it means that the interpretable model fails to explain the black box model.
Model-specific explainability techniques
In contrast to model-agnostic analysis, such as the methods we saw above, model-specific analysis focuses on the interpretation of specific models (like neural networks), using core components of the model (such as neurons and weights in neural networks) to interpret predictions. This makes model-specific methods better suited for identifying granular aspects of ML models, albeit at the cost of flexibility.
In this part, we’ll demonstrate how each method is used. The point is to show the process of model analysis, even if the model is updated over time.
Sensitivity analysis (SA)
Sensitivity analysis is a technique to assess the impact of changes in the input on the output of the AI model. It can be used to understand the contribution of individual features to the model’s predictions.
To demonstrate sensitivity analysis, we load the California Housing Dataset and use the RandomForestRegressor() class to train a model on the training data. The dataset is publically available in scikit-learn, a machine learning library in Python, and commonly used for regression analysis and predictive modeling tasks. It provides information about housing prices and related features such as the median income of households (MedInc) and the median age of houses (HouseAge) across different districts in California.
The problem is then established for sensitivity analysis, including the features and their names as shown in the code snippet below. To create N samples from the stated problem, we use the Saltelli sampling method from the SALib package. Lastly, we run the Sobol sensitivity analysis using the SALib library's sobol.analyze() function. For each feature, the function returns the first-order and total sensitivity indices.
First-order sensitivity indices provide insights into the main effects of each feature on the model’s predictions, indicating how much the output would change if only that particular feature is varied while keeping all others constant. Total sensitivity indices, on the other hand, provide a more comprehensive assessment of the impact of each feature, accounting for all possible interactions with other features.
import numpy as np from SALib.sample import saltelli from SALib.analyze import sobol from sklearn.datasets import fetch_california_housing from sklearn.ensemble import RandomForestRegressor from sklearn.model_selection import train_test_split # Load the Boston Housing dataset housing = fetch_california_housing() # Split the data into training and testing sets X_train, X_test, y_train, y_test = train_test_split(housing.data, housing.target, test_size=0.2, random_state=42) # Train a random forest model model = RandomForestRegressor(n_estimators=100, random_state=42) model.fit(X_train, y_train) # Define the problem for sensitivity analysis problem = { 'num_vars': X_train.shape[1], 'names': housing.feature_names, 'bounds': [ [X_train[:, i].min(), X_train[:, i].max()] for i in range(X_train.shape[1]) ] } # Generate samples using Saltelli sampling N = 1000 samples = saltelli.sample(problem, N) # Evaluate the model for each sample Y = model.predict(samples) # Perform Sobol sensitivity analysis Si = sobol.analyze(problem, Y, print_to_console=False) # Plot the first-order sensitivity indices fig, ax = plt.subplots() ax.bar(problem['names'], Si['S1']) ax.set_xticklabels(problem['names'], rotation=45, ha='right') ax.set_ylabel('First-order sensitivity indices') plt.show() # Plot the total sensitivity indices fig, ax = plt.subplots() ax.bar(problem['names'], Si['ST']) ax.set_xticklabels(problem['names'], rotation=45, ha='right') ax.set_ylabel('Total sensitivity indices') plt.show()


First-order sensitivity analysis of features on the model outcome


Total sensitivity analysis of features on the model outcome
The first-order sensitivity and total sensitivity analysis results are shown in the two graphs above. From both figures, it can be concluded that the feature MedInc has the greatest influence on the model’s outcome. When the feature is considered independently (first-order sensitivity analysis), the model’s output variance is 80 percent. It’s even higher (over 80 percent) when the interactions of the feature MedInc with the other features are taken into account. In contrast, the block group population (feature Population) doesn’t seem to have any impact on the model’s prediction, as both figures show an output variance of zero percent for this particular feature.
Layer-wise Relevance Propagation (LRP)
Layer-Wise Relevance Propagation (LRP) is an XAI method that can be applied to neural networks. The method shows which input features contribute most to the network’s prediction by using the trained network’s weights to calculate relevances for each neuron. This is done iteratively, starting with the output neurons and propagating relevances back from layer to layer until finally obtaining relevance scores for each input neuron of the network. As input neurons can be considered as individual features, these relevances of input neurons can be translated to relevances of features to the model’s prediction.
To use LRP for XAI Analysis, we use the Python library ‘innvestigate’. We import the MNIST dataset, a widely used benchmark dataset consisting of grayscale images of handwritten digits from 0 to 9, and create a simple neural network with two dense layers (fully connected layers) in the code below. The model is then trained on the MNIST dataset, and an instance of the “innvestigate’’ LRP analyzer is created using the create_analyzer function. We choose a random test image and use the training model to predict it. The LRP analyzer is then used to compute relevance scores for the selected image, and we use Matplotlib to show both the original image and the relevance scores as a heatmap.
import keras import numpy as np import innvestigate # Load data (x_train, y_train), (x_test, y_test) = keras.datasets.mnist.load_data() x_train = x_train.reshape((60000, 784)) x_test = x_test.reshape((10000, 784)) x_train = x_train.astype('float32') / 255 x_test = x_test.astype('float32') / 255 # Define the model architecture model = keras.models.Sequential([ keras.layers.Dense(512, activation='relu', input_shape=(784,)), keras.layers.Dropout(0.2), keras.layers.Dense(10, activation='sigmoid') ]) # Compile the model model.compile( optimizer='adam', loss='sparse_categorical_crossentropy', metrics=['accuracy'] ) # Train the model model.fit(x_train, y_train, epochs=10, validation_data=(x_test, y_test)) # Create an analyzer for the trained model analyzer = innvestigate.create_analyzer('lrp.epsilon', model) # Select a random test image and get its prediction idx = np.random.randint(len(x_test)) x = x_test[idx][np.newaxis, :] pred = model.predict(x)[0] print(f"Predicted class: {np.argmax(pred)}") # Compute relevance scores using LRP analysis = analyzer.analyze(x) # Visualize the relevance scores and the original image plt.subplot(1, 2, 1) plt.imshow(x.reshape(28, 28), cmap='gray') plt.axis('off') plt.title('Input image') plt.subplot(1, 2, 2) plt.imshow(analysis.reshape(28, 28), cmap='jet') plt.axis('off') plt.title('Relevance scores') plt.show()
Output:
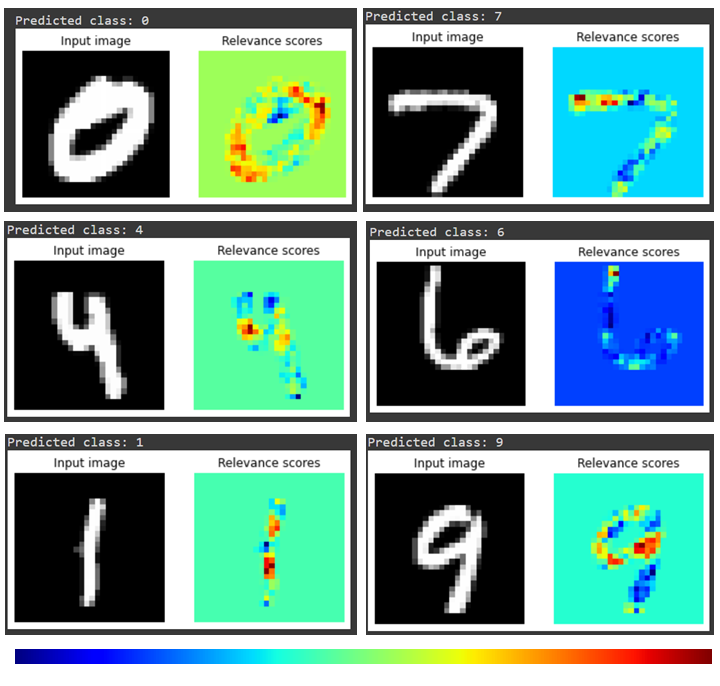

Explanation of the predicted output using the LRP method
The image above not only shows that the calculated relevance scores reveal the digits but also which parts of a digit contribute most to the model’s prediction. For instance, the lower left and upper right parts of the digit zero seem to be most relevant for the network to identify a zero in this particular image, as the color red indicates the highest relevance.

